Корреляция и Ковариация

Существует два вида зависимости между переменными величинами:

• Функциональная зависимость. Каждому значению одной переменной x соответствует СТРОГО только одно значение другой переменной y: y=f(x). (Бывают и многозначные функциональные связи, но они всегда строгие.) Такая функциональная связь имеет место только в случае, когда переменная y зависит только от переменной x и больше ни от чего. На практике, при анализе биржевых цен, таких функциональных связей не существует. Функциональная связь, это сильно упрощенная математическая модель.
• Статистическая зависимость. Каждому значению одной переменной x соответствует некоторое распределение вероятности переменной y. Например, пусть переменная y, это биржевая цена, а x, это какой-то параметр, от которого в нашей математической модели зависит цена. В этом случае на цену влияет явным образом не только значение параметра x, но и множество других факторов, которые существуют в реальности, но не учитываются упрощенной математической моделью. Многие из этих факторов являются случайными величинами.

Линейная корреляционная связь

Таких статистических связей может быть очень много самых разных. Для трейдера самым важным видом статистической связи является корреляционная связь.

Корреляционная связь, это когда каждому значению одной переменной соответствует определенное математическое ожидание другой переменной. То есть при изменении значения одной переменной, математическое ожидание другой переменной меняется закономерным образом.

А если при изменении значения одной переменной, закономерным образом меняется не только матожидание второй переменной, но и другие характеристики плотности распределения второй переменной (например, дисперсия, асимметрия и т.д.), то такая связь не является корреляционной. Хотя такая связь тоже является статистической.

Корреляционная связь между случайными переменными x и y называется линейной корреляционной связью, если матожидание переменной y линейно зависит от значений переменной x, и, одновременно, матожидание переменной x тоже линейно зависит от значений переменной y. То есть такая взаимная линейность корреляционных связей. Далее здесь рассматривается только линейная корреляционная связь.

Ковариация

Пусть математическое ожидание и дисперсия случайной величины X равны, соответственно, μ_x и σ_x². А математическое ожидание и дисперсия случайной величины Y равны, соответственно, μ_y и σ_y².

Для независимых случайных величин X и Y всегда матожидание произведения случайных величин равно произведению их матожиданий по отдельности:

M(xy) = μ_xμ_y

А для зависимых случайных величин это равенство не выполняется.

Ковариация, это отклонение математического ожидания произведения двух случайных величин от произведения их математических ожиданий:

cov(x,y) ≡ σ_xy = σ_yx = M(xy) - μ_xμ_y = M[(x-μ_x)(y-μ_y)]

Ковариация характеризует отклонение матожидания произведения двух случайных величин от произведения матожиданий этих величин. Так как это отклонение бывает только для зависимых величин, то ковариация характеризует степень этой зависимости. Чем она больше отличается от нуля, тем больше зависимость.

Матрица ковариаций для нескольких случайных величин X, Y, ..., Z всегда симметрична, причем на главной диагонали этой матрицы всегда стоят положительные числа, равные дисперсиям случайных величин X, Y, ..., Z.

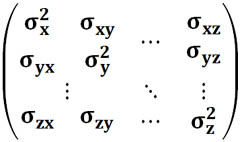
Коэффициент линейной корреляции

Ковариация неудобна тем, что имеет размерность квадрата случайных величин. Кроме того, ковариация маленькой статистической зависимости двух случайных величин с большой дисперсией (у хотя бы одной из этих величин) получается такой же, как большая статистическая зависимость у двух других случайных величин с маленькими дисперсиями. Поэтому ковариацию удобно нормировать на среднеквадратичные отклонения.

Коэффициент корреляции, это ковариация, нормированная на среднеквадратичные отклонения двух случайных величин.

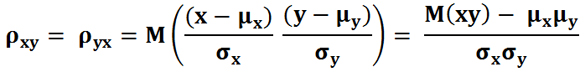
Свойства коэффициента корреляции:

1. Коэффициент корреляции может принимать значения от -1 до +1. Значения -1 и +1 этот коэффициент принимает только при линейной функциональной зависимости между X и Y. Обычно, говорят, что если коэффициент корреляции равен +1, то это абсолютно коррелирующие величины (или коррелированные на все 100%). А если коэффициент корреляции равен -1, то говорят, что это абсолютно антикоррелирующие величины (или антикоррелированные на все 100%).
2. Коэффициент корреляции между независимыми случайными величинами равен нулю. Но обратное неверно! Если коэффициент корреляции двух случайных величин равен нулю, то это ещё не означает, что эти случайные величины независимые. Они просто некоррелированные.
3. Линейные преобразования случайных величин X и Y не изменяют их коэффициента корреляции: ρ(x,y)=ρ(a+bx,c+dy)

Матрица коэффициентов корреляций для нескольких случайных величин X, Y, ..., Z всегда симметрична, причем на главной диагонали этой матрицы всегда стоят единицы.

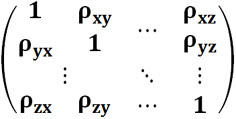
Примеры

Допустим, в каком-то эксперименте в равные промежутки времени измеряют две величины, X и Y. Если их значения меняются, как на этом графике, то это полностью коррелированные величины с коэффициентом корреляции, равным +1.

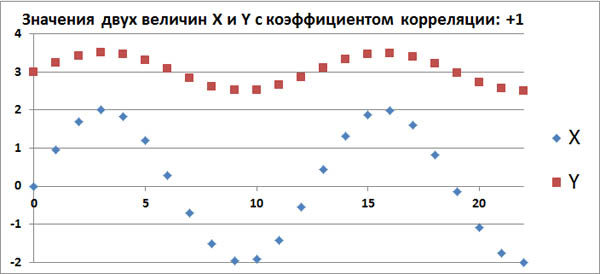
Этот факт говорит о том, что между величинами X и Y имеется строгая функциональная зависимость: Y=f(X).

Допустим, в каком-то эксперименте в равные промежутки времени измеряют две величины, X и Y. Если их значения меняются, как на следующем графике, то это полностью антикоррелированные величины с коэффициентом корреляции, равным -1.

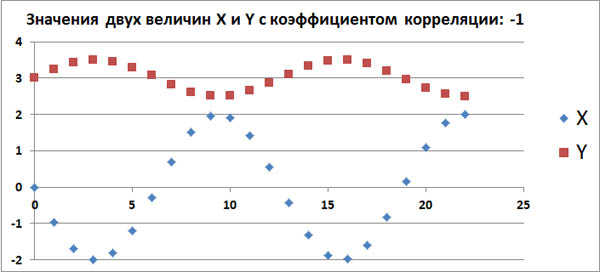
Этот факт также говорит о том, что между величинами X и Y имеется какая-то строгая функциональная зависимость: Y=g(X).

Теперь рассмотрим реальные цены. Для примера рассмотрим коэффициенты корреляции между ценами валютной пары EURUSD и ценами валютных пар GBPUSD, USDCHF и USDJPY. Для расчета возьмем дневные графики за первую половину 2017 года.

EURUSD

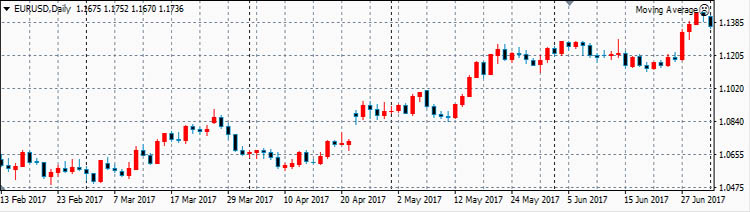
GBPUSD

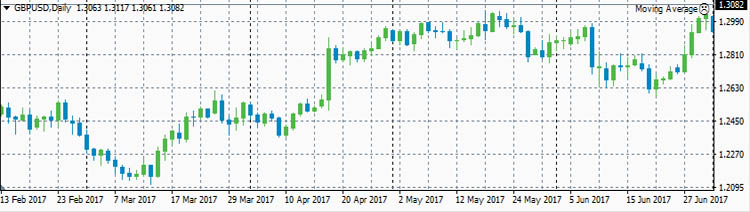
USDCHF

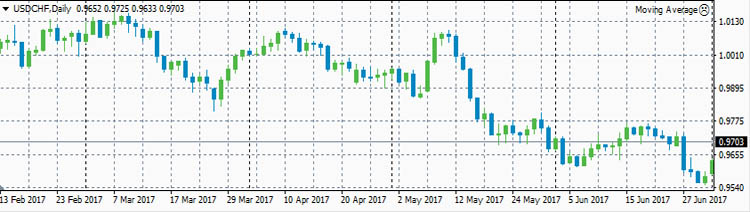
USDJPY

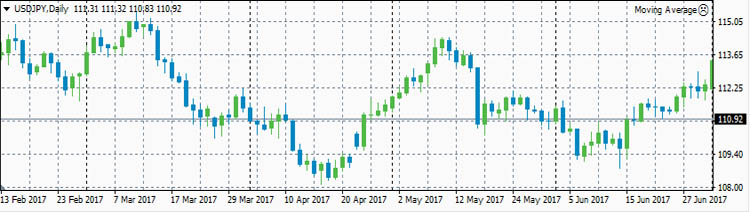
Расчеты, сделанные по ценам закрытия тайм-фреймов дают следующие коэффициенты корреляции за полгода:

• ρ(eurusd,gbpusd)=0.8030
• ρ(eurusd,usdchf)=-0.9598
• ρ(eurusd,usdjpy)=-0.4802

Эти коэффициенты корреляции достаточно ожидаемые.

Достаточно сильная корреляция между EURUSD и GBPUSD объясняется достаточно сильными связями экономики ЕвроЗоны и экономики Британии. Очень сильная антикорреляция между EURUSD и USDCHF объясняется еще более сильной связью между экономиками ЕвроЗоны и Швейцарии. А знак минус получился потому что в валютной паре USDCHF швейцарский франк стоит в знаменателе, в то время как в валютной паре EURUSD евро стоит в числителе.

Интересно посмотреть не только коэффициенты корреляции разных валютных пар, но и то, как эти коэффициенты изменяются со временем. Для этого возьмем внутри полугодового периода трехмесячный период и посмотрим, как меняется коэффициент корреляции, если сдвигать этот трехмесячный период от начала полугодового периода до его конца. Всего за полгода будет 65 таких сдвижек.

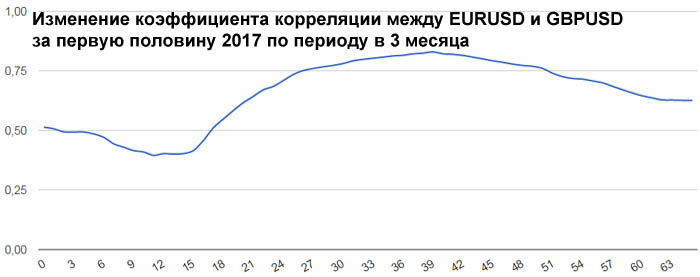
В начале 2017 года корреляция между EURUSD и GBPUSD была небольшой и она даже немного уменьшалась. Но в середине полугодия корреляция между евро и фунтом усилилась. Таким образом, в определенное время фунт может не слишком хорошо коррелировать с евро.

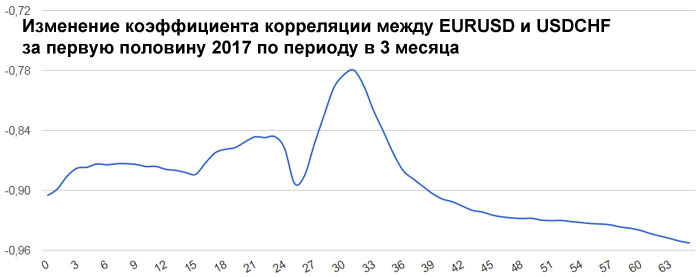
А вот в первую половину 2017 года швейцарский франк оказался привязанным к евро очень сильно. Коэффициент корреляции менялся в пределах от -0.96 до -0.78. Это и понятно, ведь Швейцария со всех сторон окружена ЕвроЗоной. Поэтому её экономика должна быть сильно связана с экономикой ЕвроЗоны. Гораздо сильнее, чем британская экономика с экономикой ЕвроЗоны.

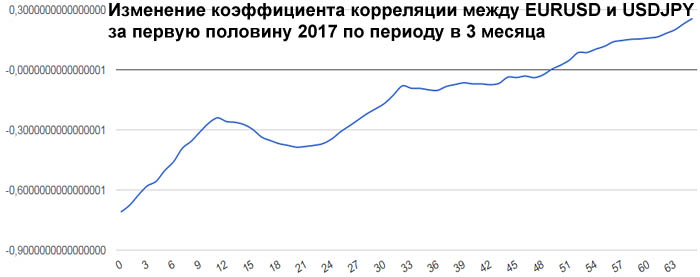
А вот что касается евро и йены, то тут ситуация самая интересная. В начале первого полугодия 2017 года была антикорреляция выше средней, примерно -0.71. Потом эта антикорреляция исчезла до нуля. Но на этом изменения коэффициента корреляции не остановились. Коэффициент корреляции вырос до +0.2564. Так как евро в валютной паре EURUSD находится в числителе, а йена в валютной паре USDJPY находится в знаменателе, то получается, что в начале года евро и йена сильно коррелировали, а к середине года стали слегка антикоррелировать.