Распределения и моменты

Закон распределения случайной величины

Для характеристики вероятности появления различных значений случайной величины используют законы распределения вероятностей случайной величины. При этом используют два вида представления законов распределения: интегральный и дифференциальный.

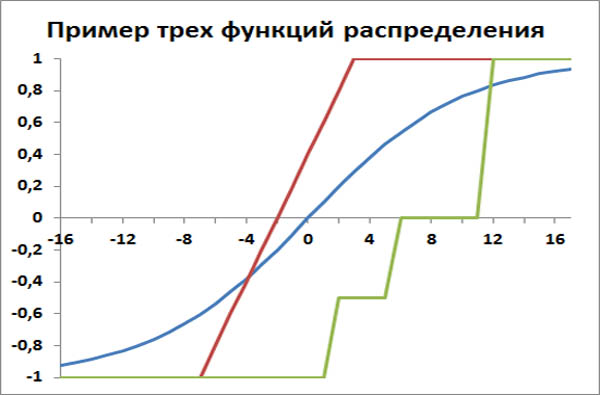
Интегральный закон, или функция распределения вероятностей случайной величины X, называется функция, значение которой для любого x является вероятностью события, заключающегося в том, что случайная величина X принимает значения, меньшие x, то есть функция F(x)=P{X<x}.

Функция распределения вероятностей F(x) имеет следующие свойства:

1. 0⩽F(x)⩽1, для любого x
2. F(x₁)⩽F(x₂), если x₁⩽x₂
3. F(-∞)=0, F(+∞)=1

Если у случайной величины функция распределения F(x) является непрерывной и дифференцируемой, то можно найти дифференциальный закон распределения вероятностей.

Дифференциальный закон, или плотность распределения вероятностей случайной величины X, называется производная функции распределения F(x), то есть p(x)=dF(x)/dx.

Плотность распределения p(x) имеет следующие свойства:

1. p(x)≥0 для любого x
2. 
   
3. 
   
4. 
   

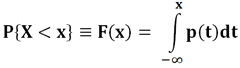
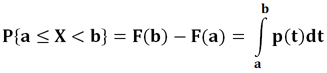
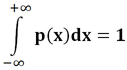
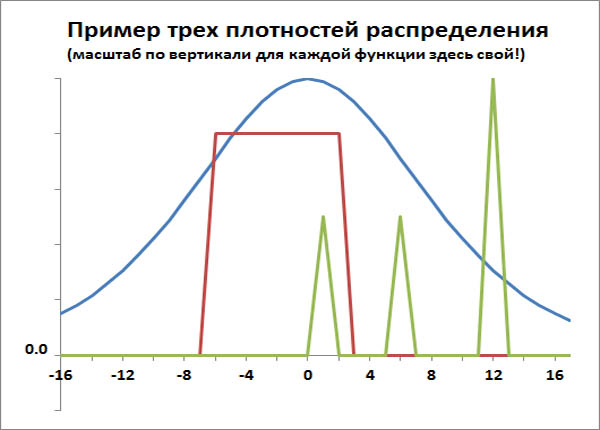
Центр распределения случайной величины

Однозначное определение понятия центра распределения не существует. Обычно, в качестве понятия центра распределения используют три понятия:

• Медиана
• Мода
• Математическое ожидание

Медиана

Медиана определяется из принципа симметрии.

Медиана, это такая точка на оси x, что слева и справа от ней вероятности появления случайной величины одинаковы и равны 1/2.

Другими словами, площадь под кривой плотности распределения справа и слева от медианы равны друг другу.

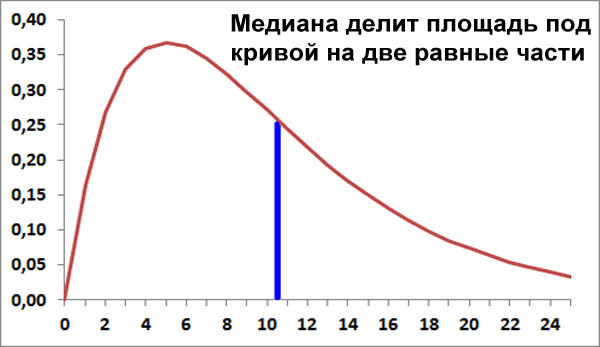
В отличие от других центров распределения, медиана существует у любого распределения вероятностей.

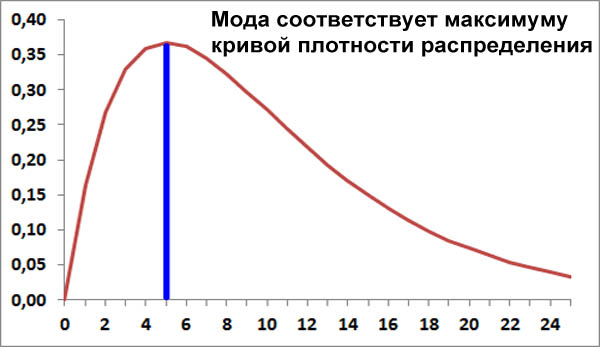
Мода

Мода, это максимум кривой плотности распределения случайной величины.

Другими словами, мода, это самое наиболее вероятное значение случайной величины, максимально вероятное.

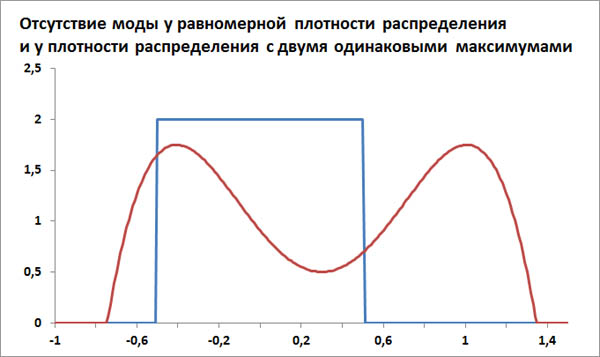
Исходя из такого определения, понятно, что мода существует не у всякого распределения. Мода не существует в случае, когда плотность распределения или не имеет максимума или у плотности распределения есть несколько максимумов одинаковой высоты. Например, у равномерного распределения, когда функция плотности распределения выглядит, как прямоугольник, нет моды.

Математическое ожидание

Чаще всего в качестве центра распределения используется математическое ожидание. Причина этого в том, что математическое ожидание можно выразить аналитически с помощью формул.

Для дискретного распределения формула математического ожидания следующая.

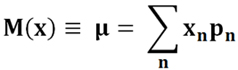
Для непрерывного распределения формула математического ожидания следующая.

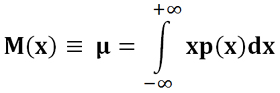
Теперь понятно, почему математическое ожидание может не существовать. Если, при стремлении x в бесконечность, плотность распределения падает как 1/x² или ещё медленнее, то интеграл в определении математического ожидания расходится.

Рассмотрим типичную задачу по вычислению математического ожидания на бинарных опционах. Допустим, брокер на выигрыш выплачивает 75% от размера ставки, а на проигрыш забирает всю ставку 100%. Найдем матожидание для метода прогнозирования, который дает 65% успешных сделок.

В работе с бинарными опционами может быть два случайных события. Это выигрыш с вероятностью p=0.65 и проигрыш с вероятностью q=0.35. Случайная величина относительного дохода трейдера (относительно величины его ставок) с вероятностью p принимает значение α=0.75 и с вероятностью q=0.35 принимает значение ß= -1.

Собираем это всё в сумму по формуле математического ожидания для дискретного распределения и получаем.

μ = αp + ßq = +0.1375

Положительное математическое ожидание говорит о том, что данный метод прогнозирования можно использовать на бинарных опционах. Трейдер будет в прибыли при большом количестве сделанных ставок, теоретически при бесконечном числе ставок (и если у него хватит начального депозита на просадки в серии проигрышей).

А если метод прогнозирования трейдера дает только 65% прибыльных сделок?

В этом случае p=0.55, q=0.45. Подставляя эти данные в формулу математического ожидания для дискретного распределения, получаем μ=-0.0375.

Отрицательное матожидание говорит о том, что данный метод прогнозирования ни в коем случае нельзя применять. Если с таким методом прогнозирования трейдер получил прибыль на конечной серии ставок, то это простое случайное везение.

Формула математического ожидания позволяет найти пограничное значение доли прибыльных сделок, которое необходимо получить от метода прогнозирования, и вывести основную формулу бинарных опционов. Основная формула бинарных опционов соответствует нулевому математическому ожиданию.

На Форексе и на фондовой бирже всё вычисляется аналогично. С той лишь разницей, что там параметры α и ß определяются через положения ордеров TakeProfit и StopLoss. Суть параметров α и ß, это доли прибыли и убытка от размера собственных средств трейдера, участвующих в сделке.

Моменты распределения

Существуют два типа моментов распределения:

• Начальный момент распределения, это момент, найденный без центрирования на математическое ожидание.
• Центральный момент распределения, это момент, найденный с учетом центрирования на математическое ожидание.

Начальный момент k-го порядка вычисляется по следующим формулам.

Для дискретного распределения:

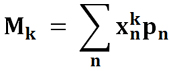
Для непрерывного распределения:

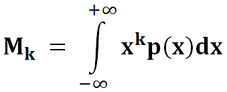
Нулевой начальный момент всегда равен единице, так как эти формулы при k=0 переходят в условия нормировки. А первый начальный момент (k=1), это как раз и есть математическое ожидание, о котором говорилось выше.

Центральный момент k-го порядка вычисляется по следующим формулам.

Для дискретного распределения:

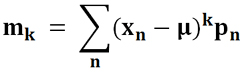
Для непрерывного распределения:

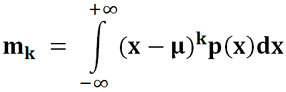
Для центральных моментов также нулевой момент всегда равен единице. А первый центральный момент всегда равен нулю. Мы, как бы, делаем такой параллельный перенос, при котором точка математического ожидания переходит в точку ноль.