Зависимость цены какого-нибудь биржевого инструмента от времени представляет собой некоторый временной ряд. Во временном ряду значения переменной известны в некоторых дискретных отсчетах времени.
Динамический ряд
Динамический ряд, это такой ряд, который представляет собой известную функциональную зависимость какой-нибудь величины от времени.
Например, Вы положили свои деньги в размере 100 тысяч рублей в банк под 6% годовых. В результате по схеме сложных процентов Вы получаете следующий временной ряд размера Вашего депозита:
- 1-й год: 106000.00 руб.
- 2-й год: 112360.00 руб.
- 3-й год: 119101.60 руб.
- 4-й год: 126247.70 руб.
Данный ряд является динамическим, так как нам хорошо известна функциональная зависимость размера депозита от времени. Она рассчитывается по формуле:
S(n) = S(0)*(1+a/100)n
Здесь n - количество лет, a - процентная ставка, S - сумма на депозите (S(0) - начальная вложенная сумма, S(n) - сумма через n лет).
Самой главной особенностью динамического ряда является то, что мы можем прогнозировать его в будущее со 100%-ной вероятностью.
Например, можем посчитать по формуле, что через пять лет на счету будет S(5)=133822.56 рублей.
В динамическом ряду размера банковского депозита есть один параметр a - процентная ставка. Если мы знаем, что, например, через три года банк уменьшит процентную ставку до 5% (допустим, это написано в договоре), то это принципиально ничего не меняет. Наш динамический ряд по прежнему очень предсказуем.
Зависимость биржевой цены от времени, конечно же, теоретически, можно считать динамическим рядом с огромным числом параметром. Но мы так считать не будем, так как на практике нам эта зависимость не известна на столько, чтобы можно было с вероятностью 100% предсказывать дальнейшее поведение цены. Нам неизвестны ни параметры этой зависимости, ни сколько их, ни то, как эти параметры сами ведут себя с течением времени.
С динамическими рядами мы чаще всего встречаемся в математических моделях физических явлений.
Случайный процесс
Случайный процесс, это такая случайная функция x(t) от независимой переменной t, что каждое испытание дает определенную функцию X(t), которая называется реализацией процесса или выборочной функцией.
Случайный процесс можно рассматривать или как совокупность реализаций процесса X(t), или как совокупность случайных величин, зависящих от параметра t. При этом должны быть заданы распределения вероятностей систем случайных величин x1=x(t1), x2=x(t2), ..., xn=x(tn) (выборочных значений) для любого конечного множества значений t1, t2, ..., tn (выборочных моментов).
Случайный процесс дискретен или непрерывен, если, соответственно, дискретно или непрерывно распределение величин x(t1), x(t2), ..., x(tn) для каждого конечного множества t1, t2, ..., tn.
Примеры.
Включаем секундомер и подбрасываем монету. Если выпадает орел, то считаем, что х=+1, если выпадает решка, то считаем, что х=-1. После 10 бросаний получаем следующую функцию X(t).
| t (сек) | 2 | 5 | 9 | 12 | 18 | 22 | 29 | 33 | 38 | 41 |
| X | 1 | 1 | 1 | -1 | 1 | 1 | 1 | -1 | -1 | -1 |
Эта конкретная функция X(t) является одной из реализаций случайной функции x(t). То есть, это выборочная функция.
Если мы еще раз подкинем 10 раз монетку, то получим другую функцию X(t), которая будет являться другой реализаций той же самой случайной функции x(t). Например, можем получить такую функцию X(t).
| t (сек) | 4 | 9 | 11 | 14 | 19 | 25 | 32 | 37 | 43 | 48 |
| X | 1 | -1 | 1 | -1 | -1 | 1 | 1 | -1 | 1 | -1 |
Мы можем изучать случайный процесс x(t) по совокупности таких реализаций X(t). Желательно, чтобы этих реализаций было как можно больше для исследования. Допустим, пригласить 100 человек и попросить их подбросить свою монету по 10 раз и записать свои результаты. У нас будет 100 выборочных функций случайного процесса.
В нашем примере для каждого значения функции x(t) задано распределение вероятности для любого t, в котором смотрим, как упала монета. У нас с вероятностью 1/2 функция x(t) принимает значение +1 и с вероятностью 1/2 принимает значение -1.
Это распределение вероятности является дискретным. Значит, в нашем примере с подбрасыванием монеты случайный процесс x(t) является дискретным.
В качестве примера непрерывного случайного процесса можно привести пример изменения какой-нибудь координаты броуновской частицы в жидкости. Допустим, измеряется вертикальная координата броуновской частицы в определенные моменты времени. Распределение вероятности в каждый такой момент времени является непрерывным.
Временной ряд
Временной ряд (или случайная последовательность), это случайный процесс, в котором независимая переменная может принимать только счетное множество значений. Таким образом, временной ряд, это частный случай случайного процесса с дискретным временем.
Например, случайный процесс изменения координаты броуновской частицы не является временным рядом. Но если мы берем координаты броуновской частицы не за всё время, а, например, только через каждую секунду, то такой случайный процесс является временным рядом.
Биржевые цены закрытия тайм-фреймов также являются временным рядом.
Наш пример из предыдущего раздела со случайным процессом x(t), который принимает значения +1 и -1, тоже является примером временного ряда, так как количество подкидываний монеты является счетным. То есть количество подкидываний монеты можно посчитать.
Если у нас стоит автомат, который постоянно подкидывает монету бесконечное число раз, например, одно подкидывание каждую секунду, то мы не можем сосчитать до конца, сколько было всего подкидываний. Но у нас есть способ подсчета этих подкидываний. Значит, количество подкидываний является счетным.
Описание случайного процесса
Для описания случайного процесса надо задать распределение величины x(t1) и все совместные распределения величин [x(t1),x(t2)], [x(t1),x(t2),x(t3], ..., [x(t1),x(t2),x(t3),...,x(tn)] для каждого конечного множества значений t1, t2, ..., tn.
Эти распределения описываются функциями распределения, соответственно, первого, второго, ..., n-ого порядков:
F(1)(X1,t1) = P{x(t1)<X1}
F(2)(X1,t1; X2,t2) = P{x(t1)<X1; x(t2)<X2}
...
F(n)(X1,t1; X2,t2; ...; Xn,tn) = P{x(t1)<X1; x(t2)<X2; ...; x(tn)<Xn}
Дискретные случайные процессы описываются вероятностями:
p(1)(X1,t1) = P{x(t1)=X1}
p(2)(X1,t1; X2,t2) = P{x(t1)=X1; x(t2)=X2}
...
p(n)(X1,t1; X2,t2; ...; Xn,tn) = P{x(t1)=X1; x(t2)=X2; ...; x(tn)=Xn}
Непрерывные случайные процессы описываются плотностями распределения:
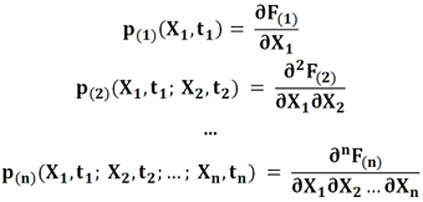
На самом деле последовательность функций распределения описывают случайный процесс с возрастающей подробностью. Ведь каждая функция распределения F(m) вполне определяет все предыдущие функции распределения F(k) для k<m.
Условная вероятность того, что в момент t1 функция x(t) принимает значение X1, в момент t2 функция x(t) принимает значение X2, ..., в момент tm функция x(t) принимает значение Xm при условии, что в момент tm+1 функция x(t) приняла значение Xm+1, ..., в момент tn функция x(t) приняла значение Xn, будет:
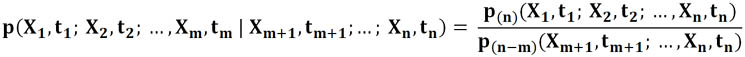
Среднее по множеству наблюдений
Среднее по множеству наблюдений для функции f(x(t1),x(t2),..,x(tn)) от n выборочных значений x(t1),x(t2),..,x(tn определяется как:
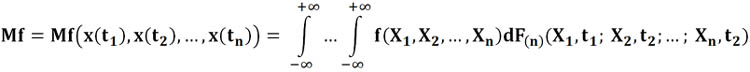
В этой формуле интегрирование идет по всем X1, X2, ..., Xn. Поэтому функция Mf, это на самом деле функция от t1, t2, ..., tn.
Корреляционная функция
Взаимная корреляционная функция двух случайных процессов x(t) и y(t) определяется как:
Rxy(t1,t2) = M[x(t1)y(t2)] - M[x(t1)]M[y(t2)] = M[( x(t1)-M[x(t1)] )( y(t2)-M[y(t2)] )]
То есть, взаимная корреляционная функция показывает отклонение среднего произведений двух случайных процессов от произведения средних этих случайных процессов.
Автокорреляционная функция
Автокорреляционная функция случайного процесса x(t) определяется как:
Rxx(t1,t2) = M[x(t1)x(t2)] - M[x(t1)]M[x(t2)] = M[( x(t1)-M[x(t1)] )( x(t2)-M[x(t2)] )]
Это то же самое, что и взаимная корреляционная функция, но берутся не два разных случайных процесса, а один и тот же случайный процесс.
Дисперсия случайного процесса
Дисперсией случайного процесса является:
D[x(t)] = M[(x(t))2] - (M[x(t)])2
Нетрудно заметить, что:
D[x(t)] = Rxх(t,t)
Ковариация случайных процессов
Ковариация двух случайных процессов x(t) и y(t) равна взаимной корреляционной функции этих процессов:
cov[x(t1),y(t2)] = Rxy(t1,t2)