Мера рассеяния

Существует два показателя того, на сколько значения случайной величины разбросаны от центра распределения:

• Дисперсия и среднеквадратичное отклонение
• Квантильное отклонение

Дисперсия и среднеквадратичное отклонение

Если математическое ожидание существует и центром распределения считать математическое ожидание, то очень удобным числовым параметром, который описывает степень разброса (рассеяния) от центра распределения, является дисперсия.

Дисперсия, это среднее значение квадратов отклонений случайной величины от её математического ожидания.

Или по другому, дисперсия, это второй центральный момент распределения. Поэтому формула дисперсии получается, если в формулу центрального момента подставить k=2.

Для дискретного распределения:

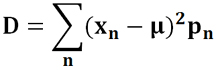
Для непрерывного распределения:

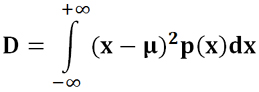
Дисперсия минимизирует средний квадрат отклонения случайной величины от ее центра. То есть, если решать задачу на минимальное суммарное отклонения средних квадратов от среднего значения, то минимум как раз и будет равен дисперсии.

Ещё одна полезная формула, которая выражает дисперсию через формулу для математического ожидания:

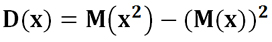
Одним из самых замечательных свойств дисперсии является её аддитивность, то есть дисперсии можно просто складывать друг с другом для случайных величин, которые статистически не зависят друг от друга. Это правило аддитивности не зависит от того, какие функции распределения имеют эти независимые величины, одинаковые или совершенно разные.

Недостатком дисперсии является то, что если функция плотности распределения убывает на бесконечности как 1/x³ или ещё медленнее, то интеграл расходится и значит, дисперсия у такого распределения не существует.

Некоторое неудобство дисперсии связано с тем, что она имеет размерность квадрата случайной величины. Поэтому более удобной характеристикой является среднеквадратичное отклонение, которое является квадратным корнем из дисперсии.

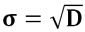
В отличие от дисперсии, у среднеквадратичного отклонения нет свойства аддитивности.

Квантильное отклонение

На практике при анализе цен трейдерам чаще придется иметь дело с квантильным отклонением при анализе меры рассеяния. В отличие от дисперсии, квантильное отклонение всегда существует для любой функции плотности распределения.

Если вероятность того, что значение случайной величины x будет меньше значения X_0.05 с вероятностью 5%, то значение X_0.05 называют 5%-ная квантиль распределения.

Аналогично, если вероятность того, что значение случайной величины x будет меньше значения X_0.95 с вероятностью 95%, то значение X_0.95 называют 95%-ная квантиль распределения.

Исходя из этих определений квантилей распределения, получается, что медиана распределения X_0.50, это 50%-ная квантиль распределения.

Вместо чисел 5% (вероятность 0.05) и 95% (вероятность 0.95) можно взять любую другую пару чисел, симметричных относительно медианы (вероятность 0.50). Например, 10% и 90%, или 23% и 77%.

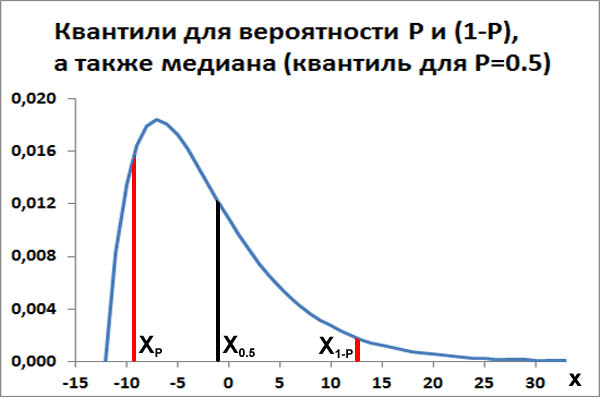
Площадь под кривой плотности распределения всегда равна единице. Медиана делит эту площадь пополам, так что справа и слева от медианы эти площади равны 1/2. А квантили симметрично отсекают справа и слева от этих площадей одинаковые площади. В этом смысле квантили всегда симметричны:

• Вероятность того, что x<X_P всегда равна вероятности того, что x>X_(1-P)
• Вероятность того, что значение переменной x попадет в интервал X_P<x<X_0.5 равна вероятности того, что её значение попадет в интервал X_0.5<x<X_(1-P)

Интервал между X_P и X_(1-P) называется интерквантильный промежуток. Например, конкретно для P=0.05 интервал значений x между X_0.05 и X_0.95 называется интерквантильный промежуток с 90%-ной вероятностью.

Пусть протяженность этого интерквантильного промежутка обозначается как Δ_0.90 = X_0.95 - X_0.05. Половина этого промежутка называется Квантильное Отклонение с 90%-ной вероятностью и обозначается как d_0.90 = Δ_0.90/2.

Квантильное отклонение применяется для оценки меры рассеяния значений случайной величины. Когда указывается квантильное отклонение, то обязательно должна быть указано и доверительная вероятность этого отклонения. В нашем примере используется 90%-ная доверительная вероятность.

Связь квантильного и среднеквадратичного отклонений

Квантильные отклонения и среднеквадратичные отклонения, в общем случае, никак не связаны друг с другом. Но есть одно исключение. Это как раз квантильное отклонение с доверительным интервалом 90%.

Для очень многих самых часто используемых функций распределения выполняется примерное равенство:

d_0.90 ≈ 1.6σ

Для других доверительных интервалов связь между d_(1-2P) и σ существенно зависит от конкретного вида функции распределения.

Поэтому, если закон распределения заранее неизвестен, как, например, для биржевых цен, то для оценки меры рассеяния следует использовать доверительный интервал 90%. С помощью последней формулы по найденному квантильному отклонению можно найти среднеквадратичное отклонение, не зная, по какому закону распределена случайная величина.