Данное введение в теорию вероятностей и математическую статистику ни в коем случае не претендует на полноту изложения. Дается только минимально необходимый материал для трейдеров, работающих на Форексе, фондовой бирже и бинарных опционах.
Данное изложение ведется на достаточно простом языке, понятным для выпусника средней школы, который не изучал эти предметы в ВУЗе. Этот материал также будет полезен тем, кто когда-то знал эти вещи, но подзабыл, и теперь надо очень быстро вспомнить хотя бы основы.
Определения
Теория вероятностей, это раздел математики, который изучает закономерности случайных событий и случайных величин, а также операции над случайными величинами.
Случайное событие, это такое событие, которое может и произойти, и не произойти при выполнении некоторых условий.
Будем считать, что эти условия могут быть воспроизведены неограниченное количество раз.
Испытанием называется каждое воспроизведение этих условий.
Закономерности
Я подкинул монету 10 раз. В результате, орел выпал 7 раз, а решка выпала 3 раза. Получилась разница 7 - 3 = 4.
Я подкинул монету 100 раз. В результате, орел выпал 56 раз, а решка выпала 54 раза. Разница получилась еще больше 56 - 44 = 12.
Я подкинул монету 1000 раз. Теперь, наоборот, орлов выпало меньше, всего 485 раз. А решек выпало 515 раз. Разница стала еще больше, но со знаком минус, так как орлов теперь меньше: 485 - 515 = -30.
Где же закономерность?
Закономерность в том, что при увеличении числа подбрасываний монеты примерно в половине случаев выпадает орел, а в половине решка, и при этом относительное отклонение от половины стремится к нулю с увеличением числа испытаний. Проверим это.
- 10 подбрасываний. 10:2=5. Абсолютные отклонения от 5: орлы 7-5=+2, решки 3-5=-2. Относительные отклонения от 5: орлы +2/5=+0.4, решки -2/5=-0.4.
- 100 подбрасываний. 100:2=50. Абсолютные отклонения от 50: орлы 56-50=+6, решки 44-50=-6. Относительные отклонения от 50: орлы +6/50=+0.12, решки -6/50=-0.12.
- 1000 подбрасываний. 1000:2=500. Абсолютные отклонения от 500: орлы 485-500=-15, решки 515-500=+15. Относительные отклонения от 500: орлы -15/500=-0.03, решки +15/500=+0.03.
Таким образом, относительное отклонение от половины резко уменьшается с ростом числа испытаний.
- 10 подбрасываний. Отклонение 40%.
- 100 подбрасываний. Отклонение 12%.
- 1000 подбрасываний. Отклонение 3%.
Вы можете провести свои испытания, и Вас получатся другие цифры. Но тенденция будет такая же.
Еще одна закономерность будет проявляться в том, что отклонений в пользу большего числа решек будет столько же, сколько отклонений в пользу большего числа орлов. Например, если проводить серию по 10 испытаний, то у меня получилось в первой серии, что орлов больше, чем решек. Но когда я провел 10 таких серий по 10 испытаний, то орлов было больше в семи сериях из 10 серий.
Затем я провел 100 серий по 10 бросаний в каждой. Теперь решек было больше в 55 серий, а орлов было больше в 45 сериях. Хотя по абсолютной величине не получается, чтобы в 50% всех серий было больше отклонений в пользу решек, а в 50% всех серий в пользу орлов, но, тем не менее, относительная разница стремиться к нулю при увеличении числа серий испытаний.
Третья закономерность, это симметрия в отклонениях в пользу решек и в пользу орлов. Если делать много серий испытаний с одинаковыми длинами этих серий, то примерно сколько раз было больше в серии орлов, столько же раз было больше и решек. И чем большее число серий сделать, тем относительная разница между большим выпадением орлов и большим выпадением решек будет стремиться к нулю.
Четвертая закономерность, это распределение отклонений от теоретического. Если провести большое число серий одинаковой длины с подбрасыванием монеты, то можно увидеть, что больше всего будет таких серий, где отклонений от 50% не будет. Поменьше будет таких серий, где отклонений от 50% будет всего на единицу. Еще меньше будет серий, где отклонений от 50% будет на 2. И так далее. Чем больше отклонение от теоретического выпадения 50% решек и 50% орлов, тем реже встречается серия подбрасываний с таким отклонением.
Относительная частота случайного события, это отношение количества случаев появления этого события M к общему числу проведенных испытаний N.
Эксперименты показывают, что при многократном повторении испытаний относительная частота M/N случайного события обладает некоторой устойчивостью. Эта устойчивость относительной частоты объясняется существованием объективных свойств и закономерностей случайного события.
Вероятность и случайная величина
Вероятность, это количественная мера наступления какого-нибудь случайного события.
Вероятность является первичным базовым понятием в математике, и ее нельзя определить через более простые термины и понятия.
Случайная величина, это такая величина, которая принимает те или иные значения с определенными вероятностями.
Вероятность может принимать значение от нуля до единицы (0⩽P⩽1). Ноль означает невозможное событие (P=0). Единица означает достоверное событие, которое обязательно случится (P=1).
Например, Вы держите в руке тяжелую гирю и выпускаете её из рук. С вероятностью P=1 гиря упадет вниз. С вероятностью P=0 гиря зависнет в воздухе как в невесомости.
Еще пример. Вы подбрасываете 6-гранный кубик с пронумерованными гранями. Два очка выпадет с вероятностью P=1/6, то есть примерно в каждом шестом испытании. Пять очков тоже выпадет с вероятностью P=1/6, то есть тоже в каждом шестом испытании.
А теперь более хитрый пример. Вы подбрасываете монету. Вероятность выпадения решки равна вероятности выпадения орла. И та и другая вероятность равна половине (P=1/2).
А может ли монета после подбрасывания встать вертикально на ребро? В прошлом примере мы считали, что это невозможное событие, то есть вероятность такого события P=0. Однако, теоретически такое случайное событие может произойти. Но вероятность такого случайного события очень-очень маленькая. Возможно, более вероятно, что Вам на голову когда-нибудь упадет метеорит, чем Вы увидите, как после подбрасывания, монета встала на своё ребро.
Пусть вероятность того, что монета встанет на своё ребро будет P=0.0000002. (Это на самом деле не так, это число взято только для примера.) Чему тогда равна вероятность выпадения орла?
Эта вероятность уже не будет равной P=0.5, так как сумма вероятности всех возможных событий не может быть равной чему-то больше единицы. В самом деле, если мы подбрасываем монету, то или выпадет решка или выпадет орел или она встанет на ребро. Ничего другого не случится. Значит, вероятность выпадения решки или орла или ребра будет равна единице (P=1). Достоверно произойдет одно из трех событий.
Поэтому, в силу симметрии между решкой и орлом, получаем, что вероятность выпадения орла будет P=0.4999999. И такая же будет вероятность выпадения решки.
0.4999999 + 0.4999999 + 0.0000002 = 1.
А если монета не может становиться на ребро, то
0.5 + 0.5 = 1.
Для 6-гранного кубика вероятность выпадения каждой из его граней P=1/6. Значит, вероятность того, что выпадет хотя бы одна грань (а это достоверное событие, которое обязательно произойдет) будет
1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
Дискретные и непрерывные случайные величины
Случайные величины могут быть дискретными и непрерывными.
Дискретная случайная величина, это такая величина, все возможные значения которой образуют конечную или бесконечную последовательность чисел (x1,x2,...,xn) и принятие ей каждого из указанных значений есть случайное событие, характеризующееся соответствующей вероятностью (P1,P2,...,Pn).
При этом выполняется условие нормировки на единицу, то есть сумма всех этих вероятностей должна быть равна единице.
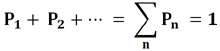
Непрерывная случайная величина, это такая величина, все возможные значения которой целиком заполняют некоторый промежуток и попадание в любой интервал (x1,x2) есть случайное событие, характеризующееся соответствующей вероятностью P{x1⩽x⩽x2}.
При этом также выполняется условие нормировки на единицу, то есть вероятность достоверного события равна единице.
P{-∞⩽x⩽+∞} = 1
Генеральная совокупность, это все возможные значения, которые может принимать случайная величина.
Сложение и умножение вероятностей
Для вычисления вероятности сложного события используют вероятности более простых событий и математические действия над ними.
Когда вероятности надо складывать, а когда их надо умножать?
Правило очень простое. Если при формулировке задачи можно использовать союз "ИЛИ", значит, вероятности надо складывать. Если при формулировке задачи можно использовать союз "И", значит, вероятности надо умножать. Посмотрим примеры с подбрасыванием 6-гранного кубика.
Какова вероятность того, что, при подбрасывании кубика, выпадет двойка или пятерка?
Используется союз "или". Значит, нужно сложить вероятность выпадения двойки с вероятностью выпадения пятерки.
P = 1/6 +1/6 = 1/3. То есть примерно треть всех подбрасываний кубиков будет приводить к тому, что выпадет или 2 или 5.
Какова вероятность того, что, при подбрасывании двух кубиков, на одном выпадет двойка, а на другом пятерка?
Можно эту задачу переформулировать через союз "и". Какова вероятность того, что, при подбрасывании двух кубиков, на одном выпадет двойка и на другом выпадет пятерка? (Союз "или" совершенно неуместен.)
Значит, нужно перемножить вероятность выпадения двойки и вероятность выпадения пятерки.
P = 1/6 x 1/6 = 1/36. То есть примерно в каждом 36-м случае всех подбрасываний кубиков будет одновременно выскакивать 2 и 5.
Аналогичная задача с таким же решением. Какова вероятность того, что, при двух подбрасываниях одного и того же кубика, один раз выпадет двойка, а второй раз выпадет пятерка? Этот вопрос снова можно переформулировать через союз "и" не меняя сути вопроса. Например, так. Какова вероятность того, что, при двух подбрасываниях одного и того же кубика, выпадет двойка и выпадет пятерка?
Теперь более сложный пример. Какова вероятность того, что, при подбрасывании двух кубиков, сумма очков будет равна четырем?
Сумма очков может быть равной 4, если или выпадает на каждом кубике по 2 очка, или если на одном кубике выпадает 1 очко, а на другом 3 очка. Переформулируем этот вопрос через наши союзы. Какова вероятность того, что, при одновременном подбрасывании двух кубиков, на одном выпадет 2 и на другом выпадет 2 или на одном выпадет 1 и на другом выпадет 3?
Два союза "и" означает, что в формуле будет два умножения. Один союз "или" означает, что в формуле будет одно сложение. Вероятности складываются и умножаются как обычные числа. То есть, если нет скобок, то сначала делается умножение, а потом сложение. Получаем
P = 1/6 x 1/6 + 1/6 x 1/6 = 1/18. То есть примерно в каждом 18-м случае сумма очков на двух кубиках будет равна 4.
Вероятность противоположного события
Противоположное событие, это дополнительное событие. То есть такие события, что появление одного или другого является достоверным событием. Другими словами, сумма противоположных событий равна единице.
Значит, чтобы найти вероятность противоположного события к данному событию, нужно от единицы отнять вероятность данного события.
Например, пусть монета не может становиться на ребро. Значит, при подкидывании монеты может выпасть или орел или решка. Выпадение орла и выпадение решки, это два противоположных события. Если вероятность выпадения орла P=0.5, то вероятность выпадения решки будет 1 - P = 1/2.
А если монета немножко кривая и вероятность выпадения орла P=0.55, то вероятность выпадения решки будет 1 - P = 0.44.
Если подбрасываем 6-гранный кубик, то событие выпадения шестерки будет противоположным событию невыпадения шестерки. А что это за событие такое невыпадение шестерки? Это событие выпадения всего остального, кроме шестерки. То есть это событие выпадения 1 или 2 или 3 или 4 или 5.
Стоят союзы "или". Значит, нужно сложить вероятности выпадения 1, 2, 3, 4, 5 очков.
P = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 5/6. Значит, вероятность выпадения шестерки будет 1 - P = 1 - 5/6 = 1/6, как и должно быть.
Разность вероятностей
Бывает так, что какое-нибудь событие может быть подмножеством другого более широкого события. Это записывается так A⊂B. Здесь событие A является подмножеством события B.
Тогда вероятность наступления события B при ненаступлении событий A будет
P{B\A} = P{B} - P{A}.
Здесь P{B} - вероятность события B, а P{A} - вероятность события A.
Например, при подкидывании кубика событие выпадения шестерки является подмножеством события выпадения четного числа очков. Значит, чтобы найти вероятность выпадения любого четного числа очков, кроме шестерки, надо от вероятности выпадения четного числа очков отнять вероятность выпадения шестерки. Это будет
P{четное\6} = P{четное} - P{6} = 1/2 - 1/6 = 1/3. (Половина всех номеров четные, поэтому P{четное}=1/2.)
Действительно, вероятность выпадения 2 или 4 будет равна 1/6 + 1/6 = 1/3.
Сложение пересекающихся событий
Если есть событие A и событие B, то в общем случае вероятность наступления события A или события B определяется формулой
P{A+B} = P{A} + P{B} - P{AB}.
Здесь P{AB} - вероятность одновременного события A и B.
Например, пусть событие A, это выпадение четного числа очков при подбрасывания кубика, а B, это выпадение маленького числа очков, то есть 1, 2 или 3 очка. Вероятность выпадения четного числа P{A}=1/2. Вероятность выпадения маленького числа очков P{B}=1/2. Нужно найти вероятность выпадения или четного числа очков или маленького числа очков.
Просто сложить эти две вероятности нельзя, так как эти два события совместимы. Если выпадет двойка, то значит, что одновременно выпало и четное число очков, и маленькое число очков. Поэтому при простом сложении вероятностей будет дважды учтена вероятность выпадения двойки. Значит, нужно от простой суммы вероятностей отнять вероятность одновременного события. Вероятность выпадения двойки P{AB}=1/6. Итак
P{A+B} = 1/2 + 1/2 - 1/6 = 5/6.